Avant l’orage, dans un coin de campagne miraculeusement épargné (pour combien de temps?) de la proche banlieue.

Au cours hebdomadaire d’anglais, attentive et concentrée. Elle a un côté Juliette Gréco, que (comme dit la chanson) les moins de 20 ans ne peuvent pas connaître. Moi non plus, mais j’en ai entendu parler.

Chien dans les hautes herbes, à l’oppidum d’Ambrussum.

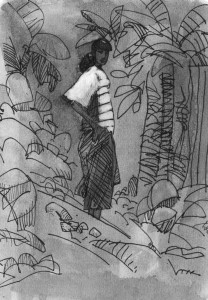Rencontre impromptue dans la forêt de Corcovado au Costa Rica.

Papilio pectore numen, espèce diurne, principalement présente en bord de mer et dans les zones côtières de l’Europe méridionale et de l’hémisphère sud. Ce papillon au thorax impressionnant, se reproduit vraisemblablement par parthénogenèse, car le mâle est inconnu. Sa chenille, dont l’activité est uniquement nocturne, peut être toxique si on en abuse. Pour une bonne conservation, les mesures habituelles (boîte vitrée hermétiquement fermée et antiseptique à la créosote) sont à appliquer.

Papilio corpus tabula (en photo spécimen femelle), espèce diurne, présente en Europe méridionale et dans les zones tropicales de l’hémisphère sud. Ce papillon qui se rencontre presque uniquement en bord de mer, n’est pas rare mais son activité est limitée à la période estivale. Sa chenille, dont l’activité est essentiellement nocturne, peut être dangereuse. A  conserver dans une boîte vitrée hermétiquement fermée et aseptisée par une fiole de créosote.

Soldat français en OPEX (opération extérieure).

Sachant que la Terre tourne autour du Soleil suivant une orbite elliptique dont la périhélie est de 0,98329 unités astronomiques et l’aphélie est de 1,0167 UA, que l’unité astronomique est définie comme ayant une valeur de 149 597 870 km, que le match de tennis a lieu un 21 juin, que notre champion renvoie la balle dans l’angle gauche du terrain de son adversaire, que jusqu’au passage au-dessus du filet – dont la hauteur réglementaire suivant les normes fédérales est de 3 pieds soit 0,914 m – le vent a chuté et qu’en raison du sens de déplacement de la balle par rapport au déplacement de la Terre, la résistance de l’air est considérée comme négligeable, mais qu’au-delà du filet une soudaine rafale de vent provenant des flancs du volcan Guagua Pichincha et soufflant à la vitesse de 17 m/s, a affecté la vitesse de déplacement de la balle d’un coefficient de 0,91.

Compte-tenu de l’énoncé du problème précédent, à quelle heure précise, le point vainqueur sera-t-il marqué ?

Sachant que la Terre qui a un diamètre équatorial de 12756,28 km, effectue une rotation sur elle-même à la vitesse de 1674,364 km/h, que sa vitesse orbitale autour du soleil est de 107218,80 km/h, que le match de tennis se déroule à Quito, capitale de l’Équateur dont l’altitude est de 2850 m, que le terrain de tennis  qui a, réglementairement, une longueur de 23,77 m et une largeur de 8,23 m est orienté Est/Ouest, qu’à 11h GMT l’adversaire qui est gaucher et se trouve dans l’angle droit du fond de court, a frappé la balle d’un revers croisé à la vitesse 172 km/h, qui est affectée d’un coefficient de 0,82 en raison de la résistance de l’air et d’un vent latéral  soufflant à la vitesse de 10m/s provoqué par la proximité du volcan Guagua Pichincha, que notre champion se trouve sur la ligne de service à une distance de 6,40m du filet, que son redoutable coup droit qui atteint la vitesse de 187 km/h est affectée d’un coefficient de 0,93 en raison du début d’une épicondylalgie du coude.

A quelle heure précise (en heure, minutes et secondes), la balle victorieuse sera-t-elle frappée?

Même le génial savant  Albert Einstein, n’a pas résolu ce problème, car il ne pratiquait pas le tennis mais jouait seulement du violon et de plus sans chaussettes.

Y… au réveil. Il ne faut surtout pas la bousculer.